Мозг продолжает удивлять нас своей великолепной сложностью. Новаторские исследования, сочетающие нейробиологию с математикой, свидетельствуют о том, что когда мозг обрабатывает информацию, он создает нейронные структуры до 11 измерений. Под «измерениями» ученые подразумевают абстрактные математические пространства, а не другие физические области. Тем не менее, исследователи «нашли мир, который мы себе не представляли», сказал Big Think Генри Маркрам, директор проекта Blue Brain, автор нового открытия.

Работа мозга – величайшая загадка науки

Мозг строит песчаные замки

Цель проекта Blue Brain, который базируется в Швейцарии, заключается в цифровом создании “биологически детализированной” симуляции человеческого мозга. Создавая цифровой мозг с «беспрецедентным» уровнем биологической информации, ученые стремятся продвинуть наше понимание невероятно сложного устройства человеческого мозга, в котором насчитывается порядка 86 миллиардов нейронов.

Чтобы получить более ясное представление о том, как работает такая огромная сеть для формирования наших мыслей и действий, ученые использовали суперкомпьютеры и особую отрасль математики. Команда основывала свои текущие исследования на цифровой модели неокортекса, которую закончила в 2015 году. Исследователи хотели выяснить, как реагирует этот цифровой неокортекс, используя математическую систему алгебраической топологии. Это позволило им определить, что наш мозг постоянно создает очень сложные многомерные геометрические фигуры и пространства, которые выглядят как «песчаные замки».

Неокортекс или новая кора – это самый новый внешний отдел головного мозга или рациональный мозг. Отвечает за высшие когнитивные функции (речь, письмо, решение задач), а также управляет аналитическим и математическим мышлением.

Без использования алгебраической топологии – раздела математики, описывающего системы с любым числом измерений, визуализация многомерной сети была бы невозможна. С помощью нового математического подхода исследователи смогли увидеть высокую степень организации в том, что раньше казалось «хаотическими» паттернами нейронов.

Алгебраическая топология подобна телескопу и микроскопу одновременно: она может увеличить масштаб сети, чтобы найти скрытые структуры – деревья в лесу – и увидеть пустые пространства – поляны – все в одно и то же время.

Автор исследования Кэтрин Хесс.

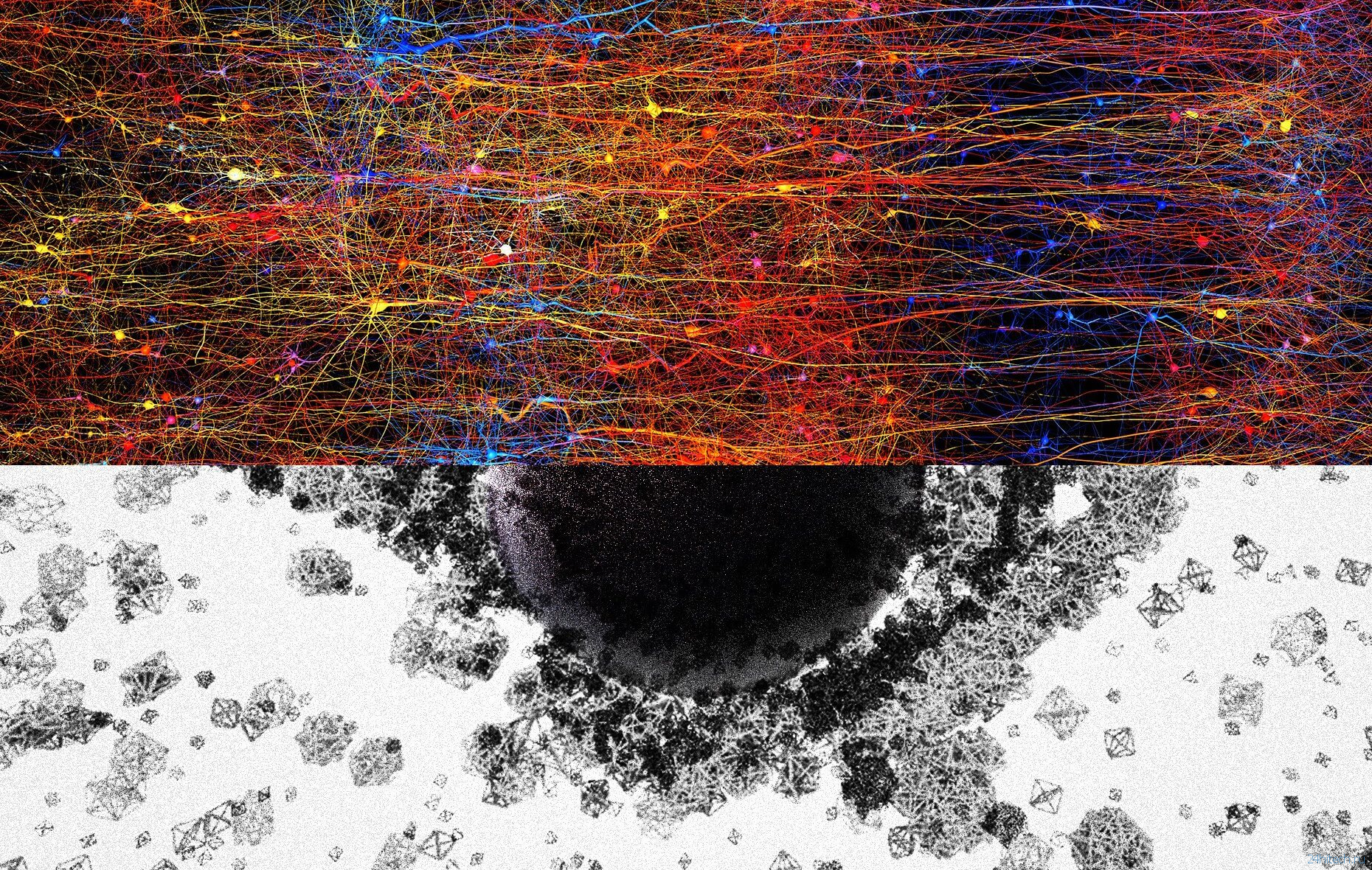
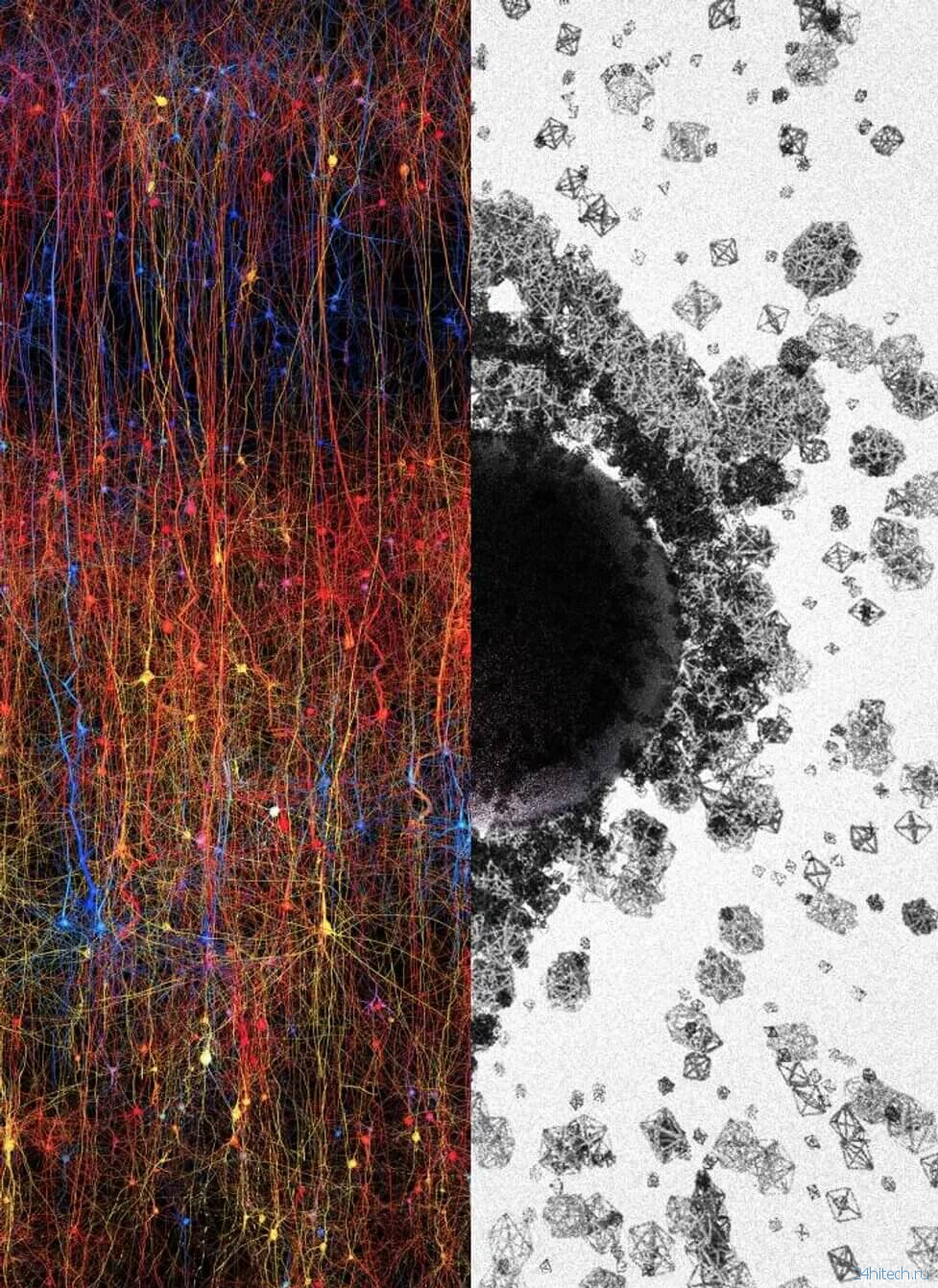
В ходе исследования ученые сначала провели тесты на созданной ими виртуальной мозговой ткани, а затем подтвердили результаты, проведя те же эксперименты на реальной мозговой ткани лабораторных крыс. При стимуляции каждый виртуальный нейрон соединяется с другим таким образом, что образуется определенный геометрический объект – клика. Большое количество нейронов добавляло больше измерений, количество которых в некоторых случаях доходили до 11. Эти структуры должны были образоваться вокруг высокоразмерной дыры, которую исследователи назвали «полостью». После того, как мозг обработал информацию, клика и полость исчезли.

Слева: цифровая копия части неокортекса, наиболее развитой части мозга. Справа: фигуры различных размеров и геометрий, представляющие собой структуры в диапазоне от 1 измерения до 7 измерений и более. «Черная дыра» в середине символизирует комплекс многомерных пространств – полости.

Появление высокоразмерных полостей, когда мозг обрабатывает информацию, означает, что нейроны в сети реагируют на стимулы чрезвычайно организованным образом. Это похоже на то, как если бы мозг реагировал на стимул, строя а затем разрушая башню из многомерных блоков, начиная со стержней (1D), затем досок (2D), затем кубов (3D), а затем более сложных геометрий с 4D, 5D и т. д. Прогрессирующая активность мозга напоминает многомерный замок из песка, который материализуется из песка и затем распадается.

Это открытие позволяет ученым глубже понять «одну из фундаментальных тайн нейробиологии — связь между структурой мозга и тем, как он обрабатывает информацию», — уточнила Кэтрин Хесс в интервью журналу Newsweek.

Исследователи надеются использовать алгебраическую топографию для изучения роли «нейропластичности», которая представляет собой процесс укрепления и ослабления нейронных связей при стимуляции — ключевой компонент процесса обучения мозга. Они видят дальнейшее применение своих открытий в изучении человеческого интеллекта и формировании памяти. Работа опубликована в журнале Frontiers in Computational Neuroscience.