Бенджамин Франклин однажды сказал, что любой дурак может критиковать, осуждать и жаловаться — и большинство дураков так и делает. Ричард Фейнман однажды сказал о научном процессе: первый принцип заключается в том, чтобы не обманывать себя — а вас легче всего обмануть. Скептики считают, что ученые могут обманывать сами себя (то ли по незнанию, то ли чтобы сохранить свое рабочее место), и зачастую обвиняют их в этом — климатологов, космологов, кого угодно. В принципе, легко отмахнуться от такой критики как от необоснованной, но возникает интересный вопрос: как мы можем убедиться, что не обманываем себя?

В науке популярно мнение, что эксперименты должно быть возможно повторить и сфальсифицировать. Если у вас есть научная модель, эта модель должна делать четкие прогнозы, и эти прогнозы должно быть можно проверить таким образом, чтобы подтвердить или опровергнуть вашу модель. Иногда критики понимают это так, что истинная наука вершится лишь в лабораторных условиях, но это лишь часть истории. Наблюдательная наука вроде космологии также подчиняется этому правилу, поскольку новые наблюдения могут потенциально опровергнуть наши текущие теории. Если, к примеру, я наблюдаю тысячу белых лебедей, я могу предположить, что все лебеди белые. Наблюдение черного лебедя изменит мои домыслы. Научная теория не может быть абсолютной, всегда носит предварительный характер, меняется при появлении новых свидетельств.

И хотя это технически правильно, называть хорошо устоявшиеся теории «предварительными» немного нечестно. Например, теория всемирного тяготения Ньютона существовала несколько веков, прежде чем ее вытеснила общая теория относительности Эйнштейна. И если мы сегодня можем сказать, что ньютонова гравитация ошибочна, она работает так же, как и всегда работала. Теперь мы знаем, что Ньютон создал приблизительную модель, описывающую гравитационное взаимодействие масс, но настолько точно приближенную к действительности, что мы и сегодня можем использовать ее для расчета орбитальных траекторий. И только когда мы расширяем свои наблюдения за пределы (очень большого) диапазона ситуаций, в которых Ньютон был прав, нам требуется помощь Эйнштейна.

Когда мы собираем доказательства, подтверждающие научную теорию, мы можем быть уверены, что она работает с небольшим окошком для новых доказательств. Другими словами, теория может считать «истинной» в диапазоне, в котором ее качественно проверяли, но новые условия могут неожиданно выявить поведение, которое приведет к более широкой и полной картинке. Наши научные теории предварительны по своей сути, но не настолько, чтобы нельзя было положиться на их точность. И в этом проблема хорошо устоявшихся теорий. Раз мы никогда не сможем узнать наверняка, что наши экспериментальные результаты — «настоящие», откуда нам знать, что мы просто не выдаем желаемый ответ за действительный?

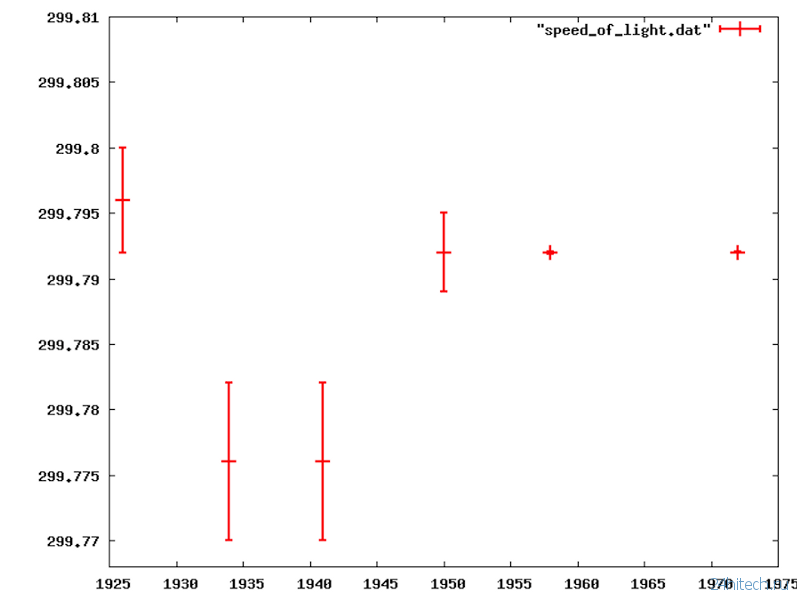
Замеры скорости света в разные годы

Такого рода мышление появляется у студентов начальных курсов. Им поручают измерить некоторые экспериментальные значения вроде ускорения силы тяжести или длины волны лазера. Будучи новичками, они зачастую делают простейшие ошибки и получают результат, который не соответствует «общепринятому» значению. Когда это происходит, они возвращаются и ищут ошибки в работе. Но если они делают такие ошибки, что они уравновешиваются или оказываются неочевидными, они не будут перепроверять свою работу. Поскольку их результат близок к ожидаемому значению, они думают, что все сделали правильно. Такое предубеждение имеется у всех нас, а иногда и у заслуженных ученых. Исторически это происходило и со скоростью света, и с зарядом электрона.

В настоящее время в космологии есть модель, которая хорошо согласуется с результатами наблюдений. Это модель ΛCDM, название которой составлено из греческой буквы «лямбда» и холодной темной материи (CDM). Большинство уточнений этой модели включают проведение более точных измерений параметров этой модели, как то возраст Вселенной, параметр Хаббла и плотность темной материи. Если модель лямбда-CDM действительно точно описывает Вселенную, то непредвзятое измерение этих параметров должно следовать статистическому шаблону. Изучая исторические значения этих параметров, мы можем измерять, насколько смещенными были измерения.

Чтобы понять, как это работает, представьте дюжину студентов, измеряющих длину меловой доски. Статистически, некоторые студенты получают значение, которое больше или меньше настоящего. Согласно обычно распределению, если реальная длина доски составляет 183 сантиметра со стандартным отклонением в сантиметр, то восемь студентов получит результат в пределах 182-184 сантиметров. Но представьте, что все студенты уложились в этот диапазон. В таком случае вы имеет право подозревать некоторые ошибки в измерениях. К примеру, студенты услышали, что доска где-то «метр восемьдесят два с половиной», поэтому проводили измерения, округляя результат к 183. Парадоксально, но если их экспериментальные результаты оказались слишком хороши, можно подозревать изначальное предубеждение при проведении эксперимента.

В космологии различные параметры хорошо известны. Поэтому когда группа ученых проводит новый эксперимент, они уже знают, какой результат общепринят. Выходит, результаты экспериментов «заражены» предыдущими результатами? Одна из последних работ Quarterly Physics Review адресована именно этому вопросу. Изучая 637 измерений 12 различных космологических параметров, они выяснили, как статистически распределены результаты. Поскольку «настоящее» значений этих параметров неизвестно, авторы использовали результаты WMAP 7 как «истинные». И выяснили, что распределение результатов было более точным, чем должно было быть. Эффект невелик, поэтому его можно было бы списать на предубежденное ожидание, но он также сильно отличался от ожидаемого эффекта, что может указывать на переоценку экспериментальных неопределенностей.

Это не значит, что наша текущая космологическая модель неверна, но значит, что нам нужно быть чуть более осторожными в своей уверенности в точности наших космологических параметров. К счастью, существуют способы повысить точность измерений. Космологи не обманывают себя и нас, просто есть еще много пространства для улучшения и исправления данных, методов и анализов, которые они используют.